Martedì mattina è stato annunciato il premio Nobel per la Fisica. Tutti si aspettavano che il premio andasse a Ronald Drever, Kip Thorne e Rainer Weiss per il progetto di LIGO atto a rilevare le onde gravitazionali, ma così non è stato. Con apparente sgomento della comunità scientifica, il Nobel è andato a David J. Thouless, F. Duncan M. Haldane e J. Michael Kosterlitz, che si sono divisi rispettivamente metà, un quarto e un quarto del premio per gli studi incentrati sugli stati topologici della materia e sulle transizioni di fase che li collegano.

Motivazioni del Comitato dei Nobel

Prima di proseguire, è bene però ricordare che la commissione per il Nobel non ha preso la decisione in modo totalmente casuale snobbando la più grande scoperta scientifica dell’anno, solo per premiare un lavoro che risale a circa una ventina di anni fa di cui non sentiva parlare nessuno, a parte gli addetti ai lavori. Il motivo della mancata premiazione della scoperta delle onde gravitazionali sarebbe da attribuire al fatto che sia stata annunciata dopo la deadline per la candidatura al Nobel, cosa che comunque prospetta le onde gravitazionali come ottimo candidato per il premio Nobel per la Fisica 2017.

Come si può vedere la notizia della rilevazione diretta delle onde gravitazionali è arrivata ben in ritardo (da un tweet di Graham Farnelo)

Tornando al premio Nobel di quest’anno, per avere un’idea del perché della sua attribuzione è bene discutere i concetti di topologia, di stato della materia e di transizione di fase.

Equivalenza Topologica

La topologia è una branca della matematica che si occupa delle proprietà dell’oggetto in considerazione, che rimangono invariate quando lo si deforma senza strapparlo, bucarlo o incollarne i lembi. Prendiamo in esame un oggetto fatto di plastilina: in base a quanto appena detto si può intuire che il numero di buchi di un oggetto sia una di queste proprietà (se volete essere precisi, invarianti topologici) e l’esempio più famoso è senza dubbio quello della tazza che si trasforma in ciambella.

Come deformare una tazza per ottenere una ciambella. (Wikipedia)

In modo perfettamente analogo, possiamo dire anche quali lettere dell’alfabeto sono equivalenti topologicamente. Le lettere Q A D R O P per esempio, saranno analoghe per il fatto che avendo un solo buco si possono deformare l’una nell’altra, cosa che non può succedere nei confronti della lettera B. Un buon esercizio è disegnare una curva chiusa sull’oggetto: se c’è un buco, vi sono delle curve particolari (come per esempio l’equatore di una ciambella) che non riuscirete mai a contrarre fino ad arrivare ad un punto; se non ve ne sono, potrete sempre farlo, e su una sfera ad esempio è facilissimo. Oltretutto, il numero di buchi è un numero necessariamente discreto: non ha senso infatti parlare di mezzi buchi.

Disegnando curve chiuse su una ciambella, non vi è modo di contrarle ad un punto. (science4all)

Stati possibili della materia

Passiamo adesso agli stati della materia: contrariamente a quanto si insegna abitualmente nella scuola dell’obbligo, essi non sono soltanto tre, e nemmeno quattro, includendo il plasma ai canonici solido, liquido e gassoso. Infatti a temperature molto basse in cui regnano gli effetti del mondo quantistico, i possibili stati della materia sono innumerevoli. Un tipo specifico di particelle, dette bosoni, hanno per esempio la caratteristica di diventare estremamente ordinati a temperature molto basse, anche se sono un gas. Per capire meglio, provate ad immaginare un gas di particelle che si muovono tutte nello stesso senso. L’altro tipo di particelle, i fermioni, sempre a temperature molto basse, riescono ad accoppiarsi e a diventare bosoni ottenendo anch’essi l’effetto precedentemente illustrato. Gli stati della materia vengono in ambito tecnico chiamati fasi: le loro transizioni sono il concetto che vogliamo spiegare.

Transizioni di fase

Torniamo però agli stati della materia più famosi, guardando lo stato liquido. Nello stato liquido, immaginando di essere una goccia di liquido, ogni posizione e direzione risulta equivalente. Ci si può muovere in qualsiasi direzione, di quanto si vuole, senza notare nessun cambiamento del panorama circostante; possiamo dire perciò che il liquido è simmetrico rispetto a ogni movimento possibile. Raffreddando però il liquido fino ad ottenere un cristallo, la situazione cambia: un cristallo ha la proprietà di essere simmetrico solo per salti discreti da un punto all’altro del reticolo che lo costituisce e con ciò si intende che non ci si rende conto della differenza se si salta da un punto all’altro del reticolo. La differenza rispetto al caso precedente è che bisogna fare il salto in una direzione particolare e di una larghezza particolare: la totale simmetria che c’era tra le direzioni spaziali è stata rotta nel passaggio da fase liquida a fase solida. Questo concetto è quasi del tutto generale per ogni transizione di fase, anche se le simmetrie rotte possono essere molto diverse.

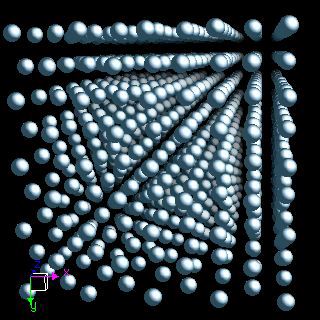
Struttura atomica del cristallo, che ne fa intuire la simmetria traslazionale (cortesia di webelements.com)

Effetti esotici delle proprietà topologiche

Restano ora da discutere i veri protagonisti in questione, gli stati della materia topologici. Nel 1980 fu scoperto un effetto, che meritò a sua volta un premio Nobel, detto effetto Hall quantistico, in cui la capacità di condurre elettricità di un materiale sottoposto a temperature bassissime o campi magnetici estremamente intensi è in grado di assumere solo valori discreti. Tali valori discreti sono legati a numeri quantici topologici, derivanti direttamente da considerazioni topologiche della materia, e tali considerazioni si rivelano essere del tutto analoghe al numero di buchi di un oggetto. Non bisogna pensare necessariamente a ciambelle in un silicato freddo, si può infatti parlare di topologia anche per caratteristiche astratte.

Gli studi proseguirono, Thouless e Kosterlitz identificarono le transizioni di fase in sistemi bidimensionali caratterizzati da difetti topologici: vortici, in poche parole. Sempre Thouless, assieme a Haldane, sviluppò i metodi per descrivere teoricamente le transizioni da una fase all’altra; l’esempio fatto durante la presentazione del Nobel trattava di uno stato della materia in cui ci sono coppie di vortici che, dopo la transizione, diventavano vortici liberi di muoversi. Il fatto che Thouless abbia collaborato a entrambi i lavori spiega la curiosa ripartizione del premio in metà per lui e un quarto rispettivamente per Haldane e per Kosterlitz.

Sebbene possa sembrare un lavoro puramente teorico, le scienze dei materiali sono un ambito in fervente sviluppo. La possibilità di spiegare effetti che possono rivelarsi molto importanti a livello microscopico (e quindi quantistico) diventa perciò un potente strumento nella ricerca e investigazione su nuovi materiali e sulle conseguenti innovazioni tecnologiche.