Lo ammetto, questo articolo sarebbe dovuto uscire alcuni giorni fa, ma ogni volta che iniziavo a scrivere, e quindi a reperire materiale, mi perdevo con le varianti (in coda all’articolo) di questo fottuto gioco che da qualche tempo sottrae a tutto il mondo preziose ore di studio.

Il vergognoso titolo di “gioco del momento” torna quindi a una griglia di numeri, dopo la mania del Sudoku: non sarò io a descrivervelo (o se preferite KnowYourMeme), vi dico solo che stavolta l’obiettivo è di ottenere il punteggio 2048 spostando e sommando le caselle numerate. Se si sfora questo preciso valore, il gioco continua e si lotta per ottenere questo numero su di una casellina.
Poniamo però che il gioco vada avanti all’infinito (come consentono alcune varianti): vi siete mai chiesti quale sia il punteggio limite? Stabilendo un paio di condizioni ideali (come fanno sempre i matematici -oh, mai una volta che ti parlino della realtà senza realizzare un modello) abbiamo provato a stabilirlo:

Il punteggio massimo è solo teorico, servirebbe una disposizione pressoché perfetta delle caselle, considerando che anche l’algoritmo del giochino in sé è un po’ una carogna nel creare la nuova casellina sempre nel posto sbagliato.

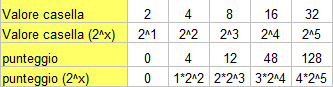
Per comporre il numero più grande possibile è necessario che ci siano sulla scacchiera tutti i sottomultipli di potenze di 2 che lo possono comporre, e poiché gli spazi sono limitati, il massimo punteggio ottenibile è quindi 2^16, ossia 65.536. Infatti, come si vede dalla foto, non c’è spazio per aumentare ulteriormente il punteggio. Ovviamente stiamo ponendo che il gioco abbia sempre fornito tessere da 2 punti.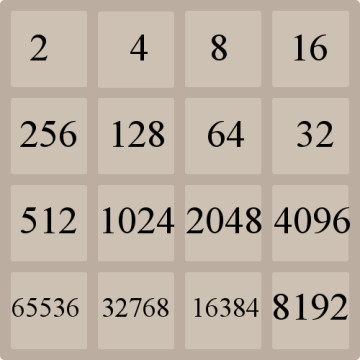

In totale, la somma di tutte le tessere massime sarà [math]\sum_{k=1}^{16} 2^k=131.070[/math] Il punteggio si calcola in maniera differente: ogni casella che viene creata sommando altre due dà come punteggio il proprio valore. Infatti una tessera “4” ha unito due tessere da 2, totale 4 punti. Ma già per creare un “8”, bisogna considerare non solo i 4+4 punti dell’unione di due tessere, ma anche dei 4 punti a testa che hanno generato le due tessere “4”. Il totale è 12 punti. Continuando il ragionamento si riesce a capire che il termine della serie generico per il punteggio è [math](n-1)*2^n[/math].

Abbiamo quindi il punteggio totale [math]\sum_{k=1}^{16} (k-1)*2^k=1.835.012[/math]

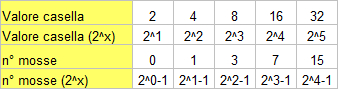
Per le mosse totali, senza considerare mosse “a vuoto”, vediamo come si comportano i primi termini e notiamo che anche qui c’è una serie ricorrente, cioè [math]2^{n-1}-1[/math]

Verranno quindi [math]\sum_{k=1}^{16} 2^{k-1}-1=65.535[/math] mosse.

Immaginiamo però che all’ultimo tentativo esca fuori una tessera da “4”: in questa maniera si potrebbero di nuovo ricombinare tutte le tessere fino ad arrivare a 2^17, ossia 131072!

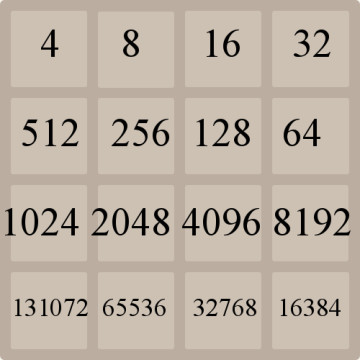
Ririempiendo di nuovo tutte le caselle, e ipotizzando che l’ultima casella sia ancora un 4, avremo una somma di caselle di [math]\sum_{k=2}^{17} 2^k=262.142[/math]

Il punteggio arriverà fino a [math]\sum_{k=2}^{17} (k-1)*2^k=3.932.164[/math]

Mentre le mosse totali saranno [math]\sum_{k=2}^{17} 2^{n-1}-1=131.054[/math] Se avete retto alla spiegazione matematica (o siete più furbi e l’avete saltata a piedi pari) vi siete meritati un po’ di svago con delle simpatiche e irresistibili varianti: quello con le regionball, quello in versione Stevie Wonder (che dimostra che anche giocando a caso si possono perdere minuti e minuti della propria vita), e il mio preferito in assoluto, LA DEGRADO EDITION, dove -ricordate- Paolo Brosio vale sempre più di Vasco Rossi…

BUON DIVERTIMENTO

Davidelo & Fisici si nasce