Condividi una Coca-Cola con….. papà, mamma, l’amico, l’amante, il cane, il bomber, Frullo ecc.

Ormai è il tormentone dell’estate, sarà una moda che ci accompagnerà per un po’ di tempo. Ho però notato che grazie a questa campagna sono tornate le lattine di forma classica, forse perché avevano degli stock in giacenza da smaltire. Questo mi ha fatto pensare alle domande che mi posi 5-6 anni fa, ai tempi del grande passaggio alle lattine slim: ma davvero le nuove sono migliori? Sprecano forse meno alluminio? La matemagica (cit.) è in grado di dare una risposta? Domande interessanti, ma mi fermarono due cose: non avevo idea dei calcoli da fare, e soprattutto non pensavo che ci potesse essere qualcuno così nerd da mettersi gratis a fare i calcoli per conto della Coca-Cola….

…..fino ad oggi, quindi eccomi qua!
In verità questo problema è già conosciuto tra gli addetti ai lavori, ma visto che i calcoli sono abbastanza semplici lo propongo a tutti. Per prima cosa, diciamo che la massima efficienza nel costruire la lattina si ha quando il rapporto tra volume e superificie è massimo, ossia: qual è la forma che consente di usare meno alluminio possibile per contenere la stessa quantità di bevanda? Semplice, la sfera. In effetti non è male l’idea di bere qualcosa da una specie di noce di cocco, ma ci sarebbero dei grossi problemi logistici. Riduciamoci quindi a parlare solo dei cilindri. Per iniziare i calcoli, scriviamo la formula della superficie e del volume interno:

Dove r è il raggio della base del cilindro, e h l’altezza.
Dobbiamo cercare ora di combinare queste due formule per ricavare qualcosa d’interessante. La superficie e il volume sono in funzione di r e h, ossia variano in base a quanto variano loro due. Il problema è che entrambe hanno sia la r che la h, e studiare le cosiddette funzioni “a due variabili” è roba da sgobboni:  non vi voglio far fare questa fine. Quindi prendiamo una strada più semplice, isoliamo h dalla seconda equazione e la schiaffiamo nella prima.

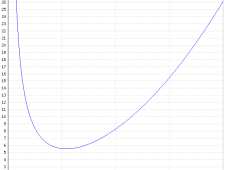
Così abbiamo una roba che varia solo con la r (Yeeee!)! Ora dobbiamo vedere quando questa “funzione superficie” è minima. Dal grafico (dove abbiamo ipotizzato il volume unitario V=1) si vede che il minimo è circa là, dove c’è la conchetta, ma provate a dire questo al vostro prof di matematica e vedete se vi risponde senza sghignazzarvi in faccia. Qua entrano in gioco per pararvi le chiappe le derivate.

La derivata è semplicemente l’inclinazione che ha la curva andando da sinistra verso destra. La linea scende, come all’inizio del grafico? La derivata è negativa. La linea sale, come alla fine? Allora è positiva (#youdontsay?). E se è stazionaria, COME SUL NOSTRO MINIMO? Allora è zero. Bene, scriviamo la derivata e la schiaffiamo uguale a zero, così capiamo dove assume tale valore!

Ma prima non avevamo detto che [math] V=\pi r^2 h[/math] ?? Allora uguagliamo le ultime due!

Alla fine scopriamo che h=2r. In pratica, la lattina che spreca meno materiale è il barattolo di mais o delle conserve di pomodoro, tanto largo quanto alto. Oltre a consumare meno, la configurazione mantiene anche meglio la temperatura della bevanda.

Ma allora perché non si usano sempre queste proporzioni per produrre le lattine?

Perché il mondo di oggi è 99% marketing. Prima di tutto, non è comodissimo cercare di bere da un barattolo così largo. Come farebbe un innocente bambino con la sua piccola mano ad afferrare la lattina per berne il contenuto? Se il gesto viene più semplice egli sarà sempre più portato a farlo, fino non farci più caso. La dipendenza da zucchero caramellato e caffeinato è così pronta per farsi spazio anche tra i giovanissimi. #gomblotto
Tranquilli, questa dipendenza non fa malissimo: l’autore di questo articolo beve un litro di cola al giorno da anni, eppure è nel peso forma e nel pieno possesso delle proprie facoltà mentali, come si può evincere dal fatto che pensa alla matematica anche davanti ad una lattina.

Tornando a noi, la lattina lunga è sottile ha secondo me dei richiami particolari: uno è riguardo agli energy drink che negli ultimi tempi spopolano a tutti i livelli, l’altro è rigurrdo i richiami sessuali. Lo so che questa riflessione fa tanto Centro Culturale San Giorgio, ma è la verità. Qualcosa di così sottile, trendy e allungato attira ben di più. In effetti, cos’è quella cosa che piace a tutti, mentre la sua controparte piace solo a molti? Sì, esattamente quello (ma io me ne dissocio: preferisco il vecchio formato di lattine). Cosa non si fa per vendere di più… addirittura dare materiale ai gomblottisti!

Come vedete, per ora le ragioni pubblicitarie hanno prevalso sulla mera matematica. Noi del Team di Fisici Si Nasce rimarremo sintonizzati per vedere cosa prevarrà fino alla fine.

Marco Pallavera – Fisici Si Nasce